Collatz Conjecture

2016-09-03, post № 140

mathematics, programming, Pygame, Python, #3n+1, #three n plus one

The Collatz conjecture states that every positive integer 𝑘 > 𝟢 will — if you iteratively set 𝑘 to 𝑓 (𝑘) — result in 𝟣 (function shown beneath).
The graph beneath shows the path length of numbers from 𝟣 to 𝟣𝟢 𝟢𝟢𝟢. In this range, 𝟨 𝟣𝟩𝟢 is the number with the most steps, 𝟤𝟨𝟣.

$f(k)={\begin{cases}\frac{k}{2}&{\text{if }}k\mod 2=0\\3\cdot k+1&{\text{if }}k\mod 2=1\end{cases}}$

Source code: collatz-conjecture.py

Curses Cam

2016-08-27, post № 139

curses, programming, Pygame, Python, #camera, #color depth, #low resolution, #shell image, #.si, #text-based images

Normally a shell lets you input via a text command and outputs via a text message^[1]. When using curses you can extend its capabilities and program for example games with limited graphics.
I wanted to go even further and built a Python script that — using Pygame’s camera module and curses — captures an image from an attached webcam (USB or built-in), transforms it and displays it on the shell.
Although both the resolution and the color depth are shrunk immensely, the resulting colored text on the shell often resembles the scene caught and has a nice visual effect.
There are two modes, camera and file viewer, which can be toggled by pressing ‘F1’. In camera mode you can see what the camera is seeing and snap a photo, which then will be saved to disk. In file viewer mode you can view the photos you took. The files will be saved in an out/ directory located in the current Python file’s directory. Saved photos have the file extension .si (“shell image”).
Unfortunately, Pygame’s camera module does neither work on Mac OS X nor on Windows. Thus this program is only properly usable under Linux^[2] systems. You obviously also need a webcam or else you will not be able to take a picture.

Controls

‘F1’ switches between camera and file viewer mode,
‘Space’ saves the current photo as a .si file (only in camera mode),
Left or down arrow key decreases current file’s id (only in file viewer mode),
Right or up arrow key increases current file’s id (only in file viewer mode).

Source code: curses-cam.py

Jetris CE

2016-08-20, post № 138

curses, games, programming, Python, #bag, #bag method, #Tetris

This game’s challenge is
to arrange the falling blocks.
Stay alive forever.

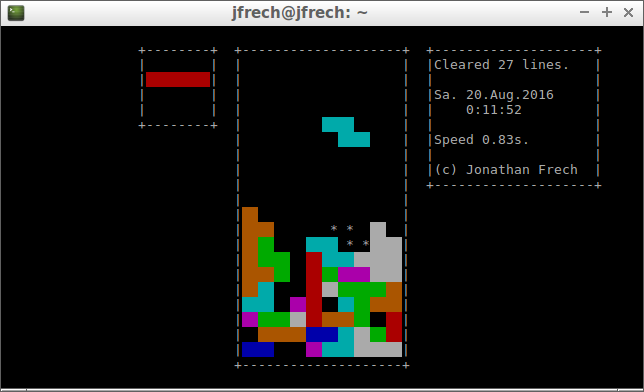
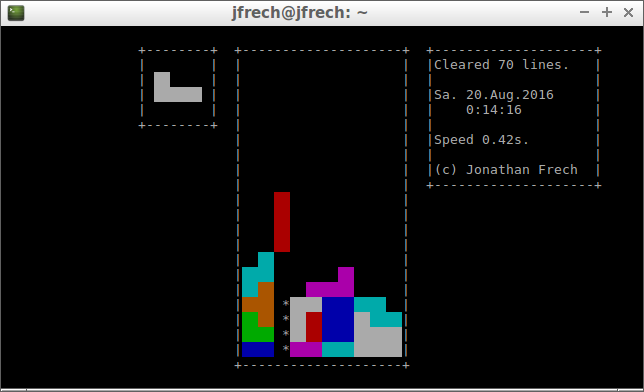
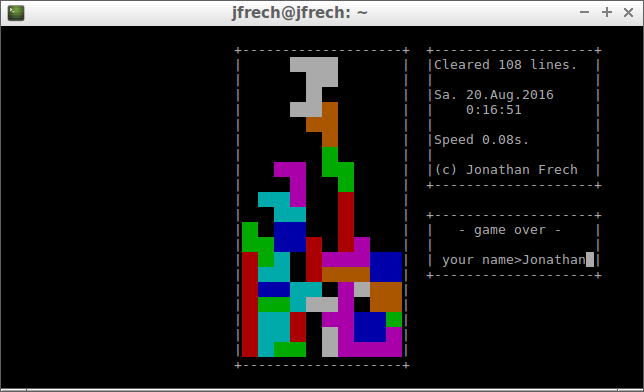
Jetris Console Edition is my second Tetris clone (see Jetris for the first one). It is programmed in Python and uses the curses module to display all its graphics on the shell.
Despite it running purely on the shell, I managed to eliminate any noticeable graphics update bugs. Furthermore the code to clear lines differs immensely from Jetris and actually works properly.
To enhance gameplay I implemented the so-called bag method. Instead of choosing pieces at random, a bag gets filled with all seven possible pieces. Each time you get a new piece, that piece gets randomly chosen out of the bag. If the bag is empty, it gets refilled. That way it is ensured that there will be no more than twelve pieces between two identical pieces (worst-case scenario). Also there will no more than four ‘S’ or ‘Z’ pieces in a row which makes the game fairer.
The pieces initially fall at one pps (pixel per second) and the game runs at twelve tps (ticks per seconds). Every ten cleared lines the speed increases by one tick or one twelfth of a second until it stays at the minimum speed, one twelfth of a second.^[1]
The game’s clock is handled by a thread and graphics updates are made when they are needed (there are no fps).
To achieve the pieces blocky look I used two spaces and a color pair whose background color is the piece’s color. On the shell two fully filled characters look like a square.
You also have the option to change your key bindings — which get saved on disk —, pause the game and there is a high score list — which also gets saved on disk. The files are located where the Python code file resides.

Source code: jetris-ce.py

Web Sudoku Solver

2016-08-13, post № 137

Auto Hotkey, games, programming, Python, #AHK, #automatic, #fast times, #good times, #web, #Web Sudoku

In my last post I used Web Sudoku to get a Sudoku as an example for my solver.

After that I wanted to automate the process of looking up a Sudoku, solving it and typing it in. But while trying to get the Sudoku’s numbers, I noticed that the whole, solved Sudoku was stored in plaintext! (Look at this page’s source code.)
So I just needed to get that information, open the Web Sudoku page in a browser and type in the already solved Sudoku.

To accomplish said goal I used the python module urllib to get the Web Sudoku page’s source code and the module webbrowser to open the page in a browser. To type in the Sudoku I used AutoHotkey.

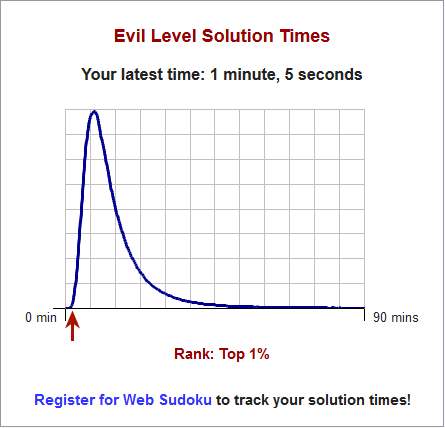
The finished program takes a level (easy, medium, hard or evil) and an id (the Sudoku’s identification number) to get a Sudoku, create an AHK file, execute it and open a web browser.
All you have to do is to click into the first box, press a key (‘F1’ in this case) and the Sudoku gets solved! You then just need to wait a minute, which is the minimum time Web Sudoku wants you to take to solve a Sudoku, and the AHK script hits enter.

You can get really good times with this:

Source code: web-sudoku-solver.py

Sudoku Solver

2016-08-06, post № 136

programming, Python, #666, #evil, #logic, #solve, #solving, #Web Sudoku

This program solves a given Sudoku.
It uses a simple strategy, looking at each box and determining those numbers that are not in its row, column and square. If that list has length 𝟣, the box’s number is determined.
After going through each box, the program generates child Sudokus in which the first empty box get filled with one of the possible numbers for that box. Sudokus with an error get eliminated.
Using this simple but effective strategy this program can solve hard Sudokus in under a second. As an example, I used Evil Puzzle 666 from Web Sudoku.
For more information on Sudokus, visit this Wikipedia entry.

Source code: sudoku-solver.py

Extra assets: sudoku-solver-2.png, sudoku-solver_bugfix-2017-12-02.py

JClock VIII

2016-07-30, post № 135

programming, Pygame, Python, #clock, #complex number, #hour, #minute, #plane, #time

Interpreting the hour hand on a clock as a two-dimensional object on a plane, the hand’s tip can be seen as a complex number.
This clock converts the hour hand’s position into a complex number, sets the number’s length to the current minutes and displays it in the form $a+b\cdot i$ .
The angle 𝜑 is determined by the hours passed ( $\frac{2\cdot\pi\cdot\text{hour}}{12}=\frac{\pi\cdot\text{hour}}{6}$ ) but has to be slightly modified because a complex number starts at the horizontal axis and turns anti-clockwise whilst an hour hand starts at the vertical axis and turns — as the name implies — clockwise. Thus, $\varphi=(2\cdot\pi-\frac{\pi\cdot\text{hour}}{6})+\frac{\pi}{2}=(\frac{15-\text{hour}}{6})\cdot\pi$ .

The complex number’s length is simply determined by the minutes passed. Because the length must not be equal to 𝟢, I simply add 𝟣: $|z|=k=\text{minute}+1$ .
Lastly, to convert a complex number of the form $k\cdot e^{\varphi\cdot i}$ into the form $a+b\cdot i$ , I use the formula $k\cdot(\cos{\varphi}+\sin{\varphi}\cdot i)=a+b\cdot i$ .

Source code: jclock-viii.py

Weekday

2016-07-23, post № 134

programming, Python, #calculation, #date, #day, #month, #time, #year

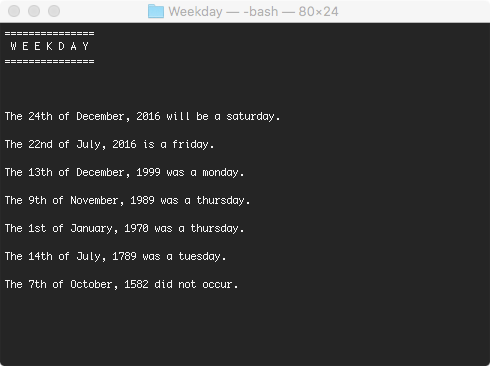
Determining the weekday based on a date composed of day, month and year.
The program counts up all the days from the 1st of January 1 to the given date, divides it by 𝟩, looks at the remainder and returns the weekday.

Source code: weekday.py

Triangular Squares

2016-07-16, post № 133

programming, Python, Wolfram Language, #equation, #number, #number theory, #numbers, #OEIS, #square, #triangle, #triangles

In a recent video, Matt Parker showed a triangular number that also is a square number, 𝟨, and asked if there were more.

A triangular number has the form $\frac{n^2+n}{2}$ — shown by Euler — and a square number has the form $m^2$ .
Triangular squares are those numbers for which $\frac{n^2+n}{2}=m^2$ with $n,m\in\mathbb{N}$ .
Examples are $\{0,1,6,35,204,1189,6930,\dots\}$ (sequence A001109 in OEIS).

To check if triangular numbers are square numbers is easy (code listed below), but a mathematical function would be nicer.
The first thing I tried was to define the triangular number’s square root as a whole number, $\sqrt{\frac{n^2+n}{2}}=\lfloor\sqrt{\frac{n^2+n}{2}}\rfloor$ . This function does not return the square numbers that are triangular but the triangular numbers that are square.
The resulting sequence is $\{0,1,8,49,288,1681,9800,\dots\}$ (sequence A001108 in OEIS).

Source code: triangular-squares.py

Posts: 292-285, 284-277, 276-269, 268-261, 260-253, 252-245, 244-237, 236-229, 228-221, 220-213, 212-205, 204-197, 196-189, 188-181, 180-173, 172-165, 164-157, 156-149, 148-141, 140-133, 132-125, 124-117, 116-109, 108-101, 100-93, 92-85, 84-77, 76-69, 68-61, 60-53, 52-45, 44-37, 36-29, 28-21, 20-13, 12-5, 4-1

Jonathan Frech's blog; built 2024/11/02 16:03:59 CET