Second Anniversary

2017-03-28, post № 165

art, #2 years, #celebration, #collage, #j, #J-Blog, #jblog, #two years

J-Blog celebrates its second anniversary!
Exactly two years ago, on the twenty-eighth of March 2015, the very first post on this blog appeared, appropriately named “Hello World”. Since then, including this one, 𝟣𝟨𝟦 other posts have been posted. Here a few of the image highlights from both years, with their corresponding post.

                     -   
            ?][)0Zqpkdc  
         QmphM&88888%av  
        Z&88%%%8M*%B8X   
       JW&Mbw\1] ZB@b    
       ?-        #BB%c   
                 m@@@kc  
                 ?o@BBC  
                  ]&@@*v 
                   L%@%Y 
                    o@BZ 
                    LB@a 
                    ]%BM?
                     *B&v
                     k%&v
                     mBWv
                     wBWv
                     ZB* 
                     w@O 
                     W8z 
                    [BO  
                    ao]  
Ckc                k&z   
b@#Z?            [a8L    
X%$@*Q[?      ?[q%&}     
 {&%%8&kwm00mdM%%w?      
  ?ZW8%%%%%%B8&q]        
    -}\wpkpft[           

Rectangles

Prime Spiral

Gradient Drawer

Pattern

Stacking Stones

Pastel

White Fireworks

Jappy Jird

Curses Cam

Maze Solving

Bifurcation Diagram

2017-03-25, post № 164

mathematics, PIL, programming, Python, #alpha, #chaos, #chaos theory, #delta, #Feigenbaum, #fractal, #iterations, #Mandelbrot set, #modelling, #population

Generating the famous fractal, which can be used to model populations with various cycles, generate pseudo-random numbers and determine one of nature’s fundamental constants, the Feigenbaum constant 𝛿.
The fractal nature comes from iteratively applying a simple function, with , and looking at its poles.
The resulting image looks mundane at first, when looking at , though the last quarter section is where the interesting things are happening (hence the image below only shows the diagram for ).
From 𝜆 = 𝟥 on, the diagram bifurcates, always doubling its number of poles, until it enters the beautiful realm of chaos and fractals.

For more on bifurcation, fractals and 𝛿, I refer to this Wikipedia entry and WolframMathworld.

Pi Day MMXVII

2017-03-14, post № 163

mathematics, programming, Python, #approximation, #dimensions, #four, #four dimensions, #generator, #higher dimensions, #hyperspheres

Every year on March the 14th, for one day the world gets irrationally excited about the famous constant 𝜋. As is tradition, you try to calculate 𝜋 in unusual ways, demonstrating the constant’s ubiquity as it crops up in the most unexpected circumstances.

           lnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
       nJ$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$w
    `v$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ 
   n$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$z 
  u$$mnn:       Y$$$i        .@$$$$$,             
 $$n           )$$$*         W$$$$$m              
-n[            $$$$.        ]$$$$$$               
              h$$$w         $$$$$$Y               
             [$$$$         X$$$$$$                
            "$$$$n        '$$$$$${                
           .$$$$$         8$$$$$$                 
           *$$$$}        :$$$$$$+                 
          #$$$$u         $$$$$$%                  
        t$$$$$$         ;$$$$$$`                  
       u$$$$$$!         $$$$$$W                   
      Y$$$$$$M         .$$$$$$,                   
    f$$$$$$$$.         Z$$$$$Z          nn        
  `w$$$$$$$$|          $$$$$$(         v$z        
 n$$$$$$$$$W           $$$$$$$1      'X$8         
Y$$$$$$$$$$            *$$$$$$$8nnnn$$$p          
$$$$$$$$$@.             W$$$$$$$$$$$$$n           
_$$$$$$${                x$$$$$$$$$0>             
   -n{.                     !|nt_.                

A fairly well-known way to approximate 𝜋 is to randomly choose points in a square (often thought of as throwing darts at a square piece of cardboard), determine their distance to a circle’s center and do a division, as I did in my 𝜋 Generator post.

However, 𝜋 does not only appear in the formula for a circle’s area, , yet^[1] also in the formula for a sphere’s volume, , and for all the infinite hyperspheres above dimension three (view this Wikipedia article for more about volumes of higher-dimensional spheres).

In particular, the formula for the hypervolume of a hypersphere in four dimensions is defined as being . Using this formula, my Python script randomly chooses four-dimensional points (each in the interval ), calculates their distance to the point and determines if they are in the hypersphere around that point with radius 𝟢.𝟧.
By dividing the number of random points which lie in the hypersphere by the number of iterations used ( in the example below), the script approximates the hypersphere’s hypervolume. By then rearranging the equation with 𝑟 = 𝟢.𝟧 to , the desired constant can be approximated.

$ python pi.py
3.14196371717

A278328

2017-03-11, post № 162

mathematics, programming, Python, #2016, #decimal reverse, #difference, #integer, #OEIS, #On-Line Encyclopedia of Integer Sequences, #palindrome, #reverse, #sequence, #square

The On-Line Encyclopedia of Integer Sequences (also known by its acronym, OEIS) is a database hosting hundreds of thousands of — as the name implies — integer sequences. Yet, despite the massive number of entries, I contributed a new integer sequence, A278328.

A278328 describes numbers whose absolute difference to their decimal reverse are square. An example would be 𝟣𝟤 or 𝟤𝟣 (both are the decimal reverse to each other), since and .

Not a whole lot is known about the sequence^[1], partly due to its definition only resulting in the sequence when using the decimal system, though it is known that there are infinitely many numbers with said property. Since there are infinitely many palindromes (numbers whose reverse is the number itself), and .

Due to there — to my knowledge — not being a direct formula for those numbers, I wrote a Python script to generate them. On the sequence’s page, I posted a program which endlessly spews them out, though I later wrote a Python two-liner, which only calculates those members of the sequence in the range from 𝟢 to 𝟫𝟪 (shown below entered in a Python shell).

>>> import math
>>> filter(lambda n:math.sqrt(abs(n-int(str(n)[::-1])))%1 == 0, range(99))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 21, 22, 23, 26, 32, 33, 34, 37, 40, 43, 44, 45, 48, 51, 54, 55, 56, 59, 62, 65, 66, 67, 73, 76, 77, 78, 84, 87, 88, 89, 90, 95, 98]

Maze Solving

2017-02-27, post № 161

programming, Python PIL, #amazing, #labyrinth, #Minotaur, #solver

Mazes have been a subject of human interest for thousands of years. The Greeks used them to trap a bull-man hybrid, the French built them to show how they could impose order on nature, and even nowadays people enjoy wandering around corn mazes.
The algorithmic art of using computers to solve mazes — and even to find the shortest path through a maze —, however, has only emerged in the last couple of decades.

I was inspired by a recent Computerphile video in which Michael Pound talks about implementing different path finding algorithms for use in maze solving. And as he used Python — one of my favourite languages out there^[1] —, I thought I could give it a try and came up with this maze solver.

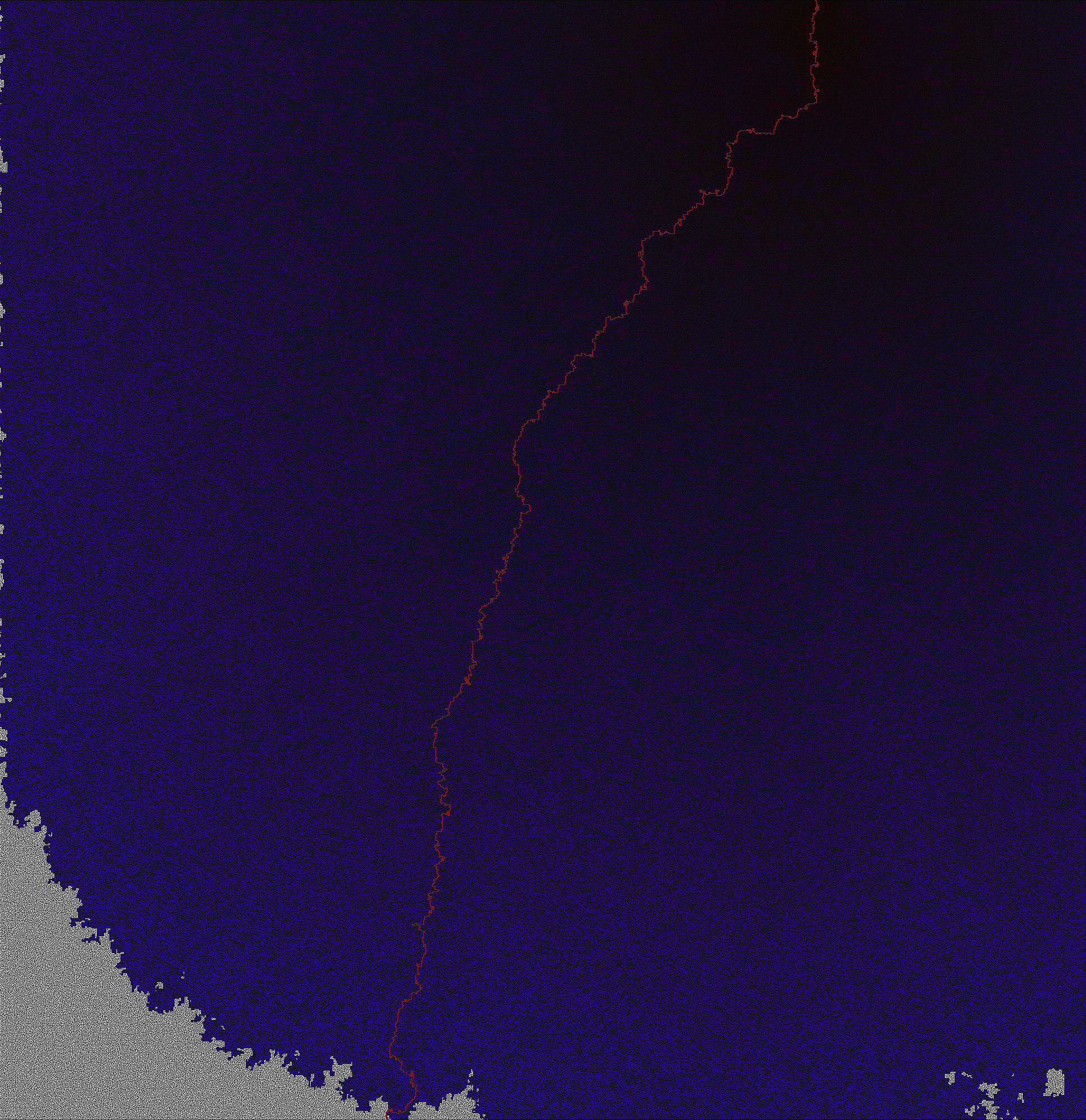
The mazes given to the solver (through a .png file) have to have a specific form. The maze needs to have a border all around (painted black) with two holes at the top and bottom, marking the maze’s start and exit (all path pixels are white).
Then the solver — using PIL — reads in the maze file, determines start and exit and starts at the maze’s start, labelling each maze path according to its shortest distance to the start. After it has found the exit, it stops looking at the maze and traces its origins back from the exit, marking the path it goes along as the maze’s optimal solution (highlighted in red).
The different hues of blue indicate the tile’s distance to the start, the white tiles are tiles the solver did not even look at.The different shadings also reveal information about the maze. Mazes with only one solution tend to have sharp changes as there are parts of the maze separated by only one wall, yet separated by a huge walk distance through the maze. The one maze with multiple solutions (see upper right image below) — in contrast — has only gradual changes in hue.

To solve a 𝟦 megapixel maze, the solver takes around 𝟥 seconds, for a 𝟣𝟨 megapixel maze around 𝟣𝟦 seconds and for a 𝟤𝟤𝟧 megapixel maze around 𝟩 minutes and 𝟤𝟤 seconds.
Performance was measured on an Intel Core i7 (𝟦.𝟢𝟢 GHz).

All mazes shown were downloaded from Michael Pound’s mazesolving GitHub repository, which were mostly generated using Daedalus.

The solver’s source code is listed below, though you can also download the .py file.

4096

2017-02-25, post № 160

games, Java, programming, #2016, #clone, #exponents, #jar, #powers of two

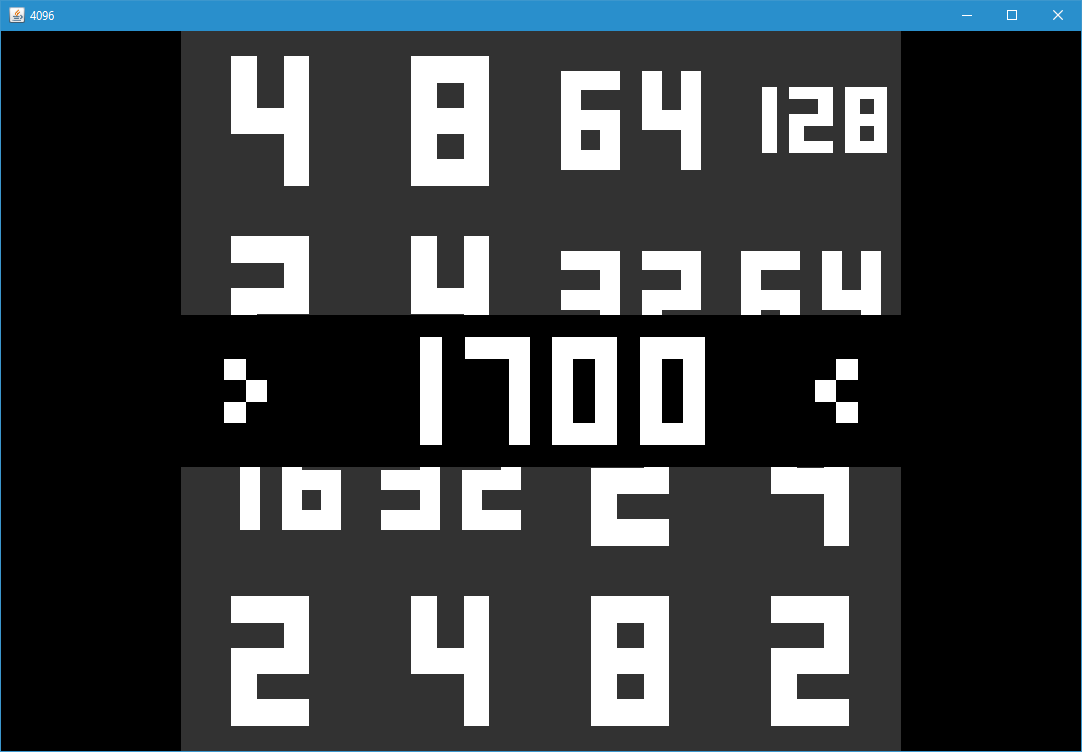
4096 is a Java-based clone of the well-known web and mobile game 2048, which itself clones 1024 and is similiar to THREES. The naming trend is quite obvious, though note that is a power of two where the exponent is divisible by three, further connecting to the aforementioned game.

In the game, you are faced with a 𝟦 ⨉ 𝟦 matrix, containing powers of two. By swiping in the four cardinal directions (e. g. pressing the arrow keys), you shove all the non-empty cells to that side. When two equal powers of two collide, they fuse together, adding. Once you shoved, an empty tile pseudo-randomly transforms to either a two-tile (𝟫𝟢％) or a four-tile (𝟣𝟢％).
Your objective at first is to reach the tile 4096, though the real goal is to achieve the highest score. Your score is the sum of all the collisions you managed to cause.

To play 4096, you can either download the .jar file or review and compile the game for yourself, using the source code listed below.

Slitherlink Solver

2017-02-11, post № 159

programming, Python, #2016, #puzzle, #shell

Slitherlink is a neat puzzle in which you are presented with a number matrix and the goal is to draw one connected, not interlooping line in between the cells. The number in each cell determines exactly how many line segments must be drawn around each cell (𝟢, 𝟣, 𝟤 or 𝟥). When a cell does not contain any number, the number of line segments adjacent to this cell are unrestricted.

*  *  *  *  *  *          *--*  *  *--*--*
     2  1  3              |  | 2  1| 3   |
*  *  *  *  *  *          *  *--*  *--*  *
        2  2  2           |     | 2  2| 2|
*  *  *  *  *  *          *--*  *--*  *  *
     2              ->       | 2   |  |  |
*  *  *  *  *  *          *  *--*  *--*  *
  1  3  1     1             1  3| 1     1|
*  *  *  *  *  *          *--*--*  *--*  *
  3     2     3           | 3     2|  | 3|
*  *  *  *  *  *          *--*--*--*  *--*

A sample 5x5 Slitherlink with solution.

Slitherlink was invented by the Japanese publisher Nikoli in 1989. It has many other names than “Slitherlink”, yet I prefer this descriptive name. Imagining a snake slithering along the board, seeking to link up with itself is a bit charming.

As with most of these puzzles that have simple rules and are fairly easy to work out by hand — on small scales that is —, writing a solver for them can prove to be more difficult than one may expect.

The first solving strategy I tried out was to brute force the problem. Using the Slitherlink from above as an example, there would be different cells with line segments. With each line segment either being drawn or not, there are different boards to check. With one board being checked per nanosecond the solver would take seconds or 𝟥𝟨.𝟧𝟨 years. Brute force is definitely not a viable way to conquer Slitherlink.

After this harsh discovery, I needed a better way to approach solving a given Slitherlink puzzle. Doing some research, I even discovered that Slitherlink is an NP-complete problem (see this paper^[1] by Stefan Herting), whereby it — assuming  — is not even possible to write a solving algorithm which takes polynomial time.
However, solving small Slitherlink puzzles is fortunately possible in a reasonable time frame.

The strategy I used in the solver consists of pre-programmed rules — figured out by humans — which determine parts of the board based on special arrangements and enforcing the puzzle’s rules (such as that there must only be one line). Using those clues, the solver partly solves a given Slitherlink until there are no more known rules to advance. At that point the solver guesses for a given line segment to be either crossed (marking it cannot be drawn) or drawn, building a tree.
Conflicting attempts (where the solver wrongly guessed, then later — through applying the given rules — determines the attempt as flawed) are thrown away, only leaving possible solved scenarios. Because each Slitherlink has one unique solution, this process ultimately results in one surviving attempt, which then is checked for correctness and printed out as the solution.
A list of Slitherlink rules can be found in this Wikipedia article.

Using the above described method, my solver takes roughly 𝟢.𝟢𝟧 seconds on an Intel Core i7 (𝟦.𝟢𝟢 GHz) to solve the example 𝟧 ⨉ 𝟧 Slitherlink. A 𝟣𝟢 ⨉ 𝟣𝟢 Slitherlink takes around 𝟣.𝟨 seconds whereas it takes 𝟥𝟤 seconds to solve a 𝟣𝟧 ⨉ 𝟣𝟧 Slitherlink. The non-polynomial time is clearly recognisable.^[2]

My solver best runs in a bash shell^[3], as it uses ANSI escape sequences to give the solved line a vivid blue and is entirely written in Python as well as fully text-based. The source code is listed below.

Other people also have written solvers, including puzzle generators, such as kakuro-online or appspot. The latter even supports different polygons as the Slitherlink base.

Double-Slit Experiment

2017-01-28, post № 158

ImageMagick, programming, Python PIL, #animation, #flight, #gif, #light, #physics

Light is a fascinating thing in our universe. We perceive it as color, warmth and vision. Yet it does things one may not expect it to do. One of the experiments that called for a better physical model of light was the double slit experiment. In this experiment, a laser is shone through two closely adjacent slits and projected on the screen behind. Using old physical models, one would expect to see one or maybe two specs of light on the screen, when in reality there appear alternating dark and bright spots.

To explain why this seemingly strange phenomenon is occurring, one can either see light as photons and comprehend that a photon presumably follows every possible path there is in the entire universe and then — through it being observed — randomly chooses one path and thus creates stripes (according to the theory of quantum mechanics) or one can see light as simply being a wave.

For more information on the double-slit experiment, I refer to this Wikipedia entry.

The animation shown below describes light as a wave. The green vectors represent the light wave’s phase at the points on the light beam, the yellow vector represents the addition of both of the slit’s light beam’s phase when hitting the screen and the red dots at the screen represent the light’s brightness at that point (defined by the yellow vector’s length).
To create the animation, Python and a Python module called PIL were used to create single frames which were then stitched together by ImageMagick to create an animated gif.