Triangular Squares

2016-07-16, post № 133

programming, Python, Wolfram Language, #equation, #number, #number theory, #numbers, #OEIS, #square, #triangle, #triangles

In a recent video, Matt Parker showed a triangular number that also is a square number, 𝟨, and asked if there were more.

A triangular number has the form $\frac{n^2+n}{2}$ — shown by Euler — and a square number has the form $m^2$ .
Triangular squares are those numbers for which $\frac{n^2+n}{2}=m^2$ with $n,m\in\mathbb{N}$ .
Examples are $\{0,1,6,35,204,1189,6930,\dots\}$ (sequence A001109 in OEIS).

To check if triangular numbers are square numbers is easy (code listed below), but a mathematical function would be nicer.
The first thing I tried was to define the triangular number’s square root as a whole number, $\sqrt{\frac{n^2+n}{2}}=\lfloor\sqrt{\frac{n^2+n}{2}}\rfloor$ . This function does not return the square numbers that are triangular but the triangular numbers that are square.
The resulting sequence is $\{0,1,8,49,288,1681,9800,\dots\}$ (sequence A001108 in OEIS).

Source code: triangular-squares.py

RGB Jallenge

2016-07-09, post № 132

games, programming, Pygame, Python, #blue, #color, #colors, #colour, #colours, #green, #guess, #guessing, #red

This is a clone of The Great RGB Guessing Challenge^[1]. The challenge works like this: You are presented three numbers ranging from 𝟢 to 𝟤𝟧𝟧 representing a rgb color and three color bubbles. To get a point you must choose the color bubble corresponding to the rgb values. The more points you get, the higher your score.

Controls

Click on the bubble to choose it.

Source code: rgb-jallenge.py

Extra assets: rgb-jallenge-0.png, rgb-jallenge-1.png, rgb-jallenge-2.png, rgb-jallenge-3.png, rgb-jallenge-4.png, rgb-jallenge-5.png, rgb-jallenge-6.png, rgb-jallenge_colors-fixed.py

Palindrome Function

2016-07-02, post № 131

mathematics, programming, Python, #p(n), #sum

To get a number’s palindrome in a programming language like python is easy. There are ways to swap between integer and string and strings can be manipulated.

>>> n = 1234
>>> int(str(n)[::-1])
4321

But I wanted to create a mathematical function 𝑝(𝑛), which returns an integer’s palindrome. Thus 𝑝(𝟣𝟤𝟥𝟦) = 𝟦𝟥𝟤𝟣.

Firstly, I needed a way of determining the number’s size. In base 𝟣𝟢 the length is calculated using the logarithm to said base.

$l(n)=\lfloor\log_{10}{n}\rfloor+1$

$l(1234)=\lfloor\log_{10}{1234}\rfloor=\lfloor 3.09\rfloor+1=4$

Secondly, I need a way to isolate a specific digit. Using the floor function, this function returns the 𝑖-th digit (starting on the right with 𝑖 = 𝟢).

$d_i(n)=\lfloor\frac{n}{10^i}\rfloor-\lfloor\frac{n}{10^{i+1}}\rfloor\cdot 10$

$d_2(1234)=\lfloor\frac{1234}{10^2}\rfloor-\lfloor\frac{1234}{10^{2+1}}\rfloor\cdot 10=\lfloor 12.34\rfloor-\lfloor 1.23\rfloor\cdot 10=12-1\cdot 10=2$

Thirdly, both of these functions can be used to split up the number into a sum.

$n=\sum\limits_{i=0}^{l(n)-1}\Big[d_i(n)\cdot 10^{i}\Big]=\sum\limits_{i=0}^{\lfloor\log_{10}{n}\rfloor}\Big[\big(\lfloor\frac{n}{10^i}\rfloor-\lfloor\frac{n}{10^{i+1}}\rfloor\cdot 10\big)\cdot 10^{i}\Big]$

Fourthly, I only need to swap the power of ten at the end to get my palindrome function.

$p(n)=\sum\limits_{i=0}^{l(n)-1}\Big[d_i(n)\cdot 10^{l(n)-1-i}\Big]=\sum\limits_{i=0}^{\lfloor\log_{10}{n}\rfloor}\Big[\big(\lfloor\frac{n}{10^i}\rfloor-\lfloor\frac{n}{10^{i+1}}\rfloor\cdot 10\big)\cdot 10^{\lfloor\log_{10}{n}\rfloor-i}\Big]$

Thus the final function 𝑝(𝑛) is defined.

$p(n)=\sum\limits_{i=0}^{\lfloor\log_{10}{n}\rfloor}\Big[\big(\lfloor\frac{n}{10^i}\rfloor-\lfloor\frac{n}{10^{i+1}}\rfloor\cdot 10\big)\cdot 10^{\lfloor\log_{10}{n}\rfloor-i}\Big]$

To check if the formula is correct, I use 𝟣𝟤𝟥𝟦 (as seen above).

$p(1234)=\sum\limits_{i=0}^{\lfloor\log_{10}{1234}\rfloor}\Big[\big(\lfloor\frac{1234}{10^i}\rfloor-\lfloor\frac{1234}{10^{i+1}}\rfloor\cdot 10\big)\cdot 10^{\lfloor\log_{10}{1234}\rfloor-i}\Big]$

$p(1234)=\sum\limits_{i=0}^{3}\Big[\big(\lfloor\frac{1234}{10^i}\rfloor-\lfloor\frac{1234}{10^{i+1}}\rfloor\cdot 10\big)\cdot 10^{3-i}\Big]$

$p(1234)=d_0(1234)\cdot 10^3+d_1(1234)\cdot 10^2+d_2(1234)\cdot 10^1+d_3(1234)\cdot 10^0$

Jimon

2016-06-25, post № 130

games, programming, Pygame, Python, #color, #color memory, #memeory, #memory game, #remember, #sequence, #Simon, #Simon Says

This game is a recreation of the famous game Simon. In the game there are four colors which form a sequence that is expanding every cycle. The aim of the game is to memorize said sequence as far as possible.For more information on the Simon game visit this Wikipedia entry.

Controls

Click on the colored buttons to press them.

Source code: jimon.py

Numerals

2016-06-18, post № 129

programming, Python, #number words, #numbers, #numbers to words, #numeral, #words

This program takes a number and calculate it’s linguistic numeral.The number 𝟥 returns the numeral ‘three’, 𝟧𝟪 returns ‘fifty-eight’ and 𝟥𝟣𝟦𝟣𝟧.𝟫𝟤𝟨𝟧𝟥𝟧 returns ‘thirty-one thousand four hundred fifteen point nine two six five three five’.

Source code: numerals.py

Leaf

2016-06-11, post № 128

art, haiku, poetry, #anim gif, #animated, #animated gif, #cliff, #fall, #foliage, #gif

A leaf on a tree
gets blown away by the wind
and falls down a cliff.

Cycloids

2016-06-04, post № 127

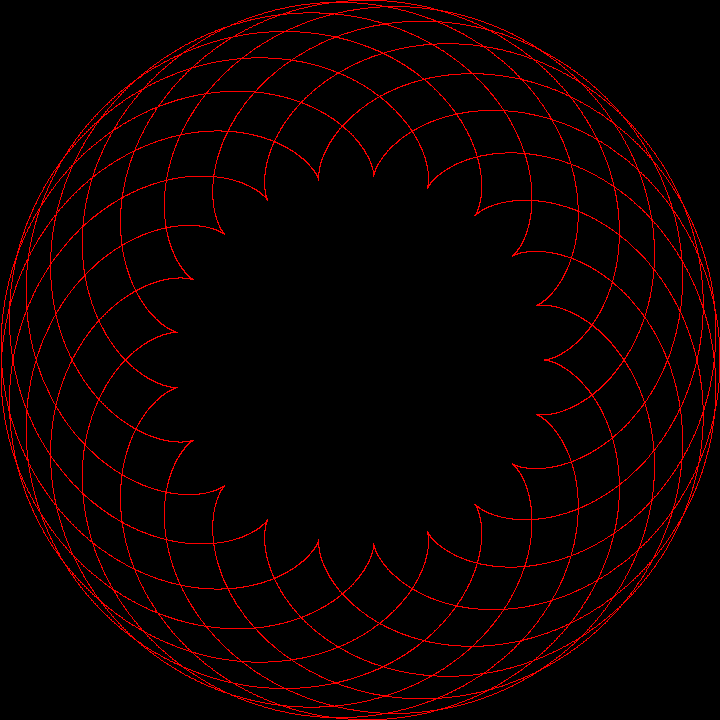
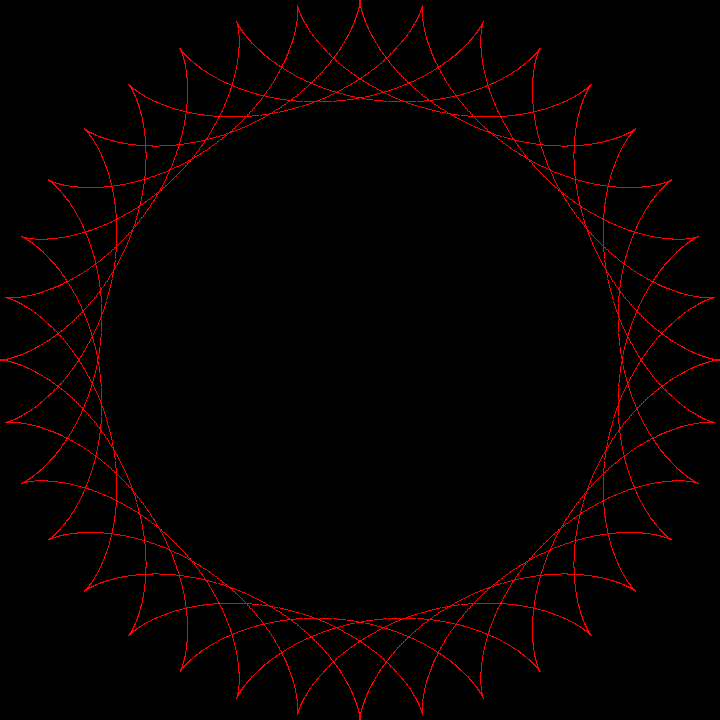
mathematics, programming, Pygame, Python, #circle, #circles, #curve, #cycloid, #epi, #epicycloid, #geometry, #hypo, #hypocycloid, #rolling, #trace

A cycloid is the curve generated by tracing a point on a smaller circle rolling around an bigger circle.
The word cycloid comes from the greek word “κύκλος” meaning “circle”. There are epicycloids and hypocycloids (smaller circle located above and beneath the bigger circle).
The cycloid is determined by the ratio between the two circle’s radii $k=\frac{R}{r}$ .
More information can be found on this Wikipedia entry.

Source code: cycloids.py

Extra assets: cycloids-0_k3_hypo.png, cycloids-1_k3_epi.png, cycloids-2_k4_hypo.png, cycloids-3_k4_epi.png, cycloids-4_k5_hypo.png, cycloids-5_k5_epi.png, cycloids-6_k6_hypo.png, cycloids-7_k6_epi.png, cycloids-10_k3.8_hypo.png, cycloids-11_k3.8_epi.png, cycloids-12_k5.5_hypo.png, cycloids-13_k5.5_epi.png, cycloids-15_k7.2_epi.png

Sierpiński TIrangle

2016-05-28, post № 126

BASIC, mathematics, programming,

Using the same method used in my previous Sierpiński Triangle program, which is written in Python, I wrote a fractal generator for my graphing calculator TI-84 Plus in BASIC.

Source code: sierpinski-tirangle.basic

Extra assets: sierpinski-tirangle.8xp, sierpinski-tirangle-1.png, sierpinski-tirangle-3.png, sierpinski-tirangle-5.png, sierpinski-tirangle-6.png, sierpinski-tirangle-7.png, sierpinski-tirangle-8.png

Posts: 293-286, 285-278, 277-270, 269-262, 261-254, 253-246, 245-238, 237-230, 229-222, 221-214, 213-206, 205-198, 197-190, 189-182, 181-174, 173-166, 165-158, 157-150, 149-142, 141-134, 133-126, 125-118, 117-110, 109-102, 101-94, 93-86, 85-78, 77-70, 69-62, 61-54, 53-46, 45-38, 37-30, 29-22, 21-14, 13-6, 5-1

Jonathan Frech's blog; built 2024/12/19 23:13:08 CET