Prime-Generating Formula

2016-04-01, post № 114

mathematics, #generating, #prime formula, #primes

(April Fools’!) I came up with this interesting prime-generating formula. It uses the constant 𝜉 and generates the primes in order!

The constant’s approximation.

The formula calculates the 𝑛-th prime.

The first few values for when starting with 𝑛 = 𝟢 are as follows.

First Anniversary

2016-03-28, post № 113

art, #1 year, #1st, #animated, #animated gif, #birthday, #celebrate, #gif, #one year

J-Blog celebrates its first anniversary!

Happy Easter II

2016-03-27, post № 112

art, #animated, #animated gif, #bunny, #celebrating, #celebrating easter, #chicken, #egg, #gif, #present, #rabbit

Little pixel guy wishes you a happy easter!

Pascal’s Triangle

2016-03-26, post № 111

mathematics, programming, Pygame, Python, #crown, #generate, #sequence

Pascal’s triangle is an interesting mathematical sequence. It is often written as a triangle, starting with , then . To generate the next row, you add the two numbers above to form another one. So the next row in the sequence is then , and so on (sequence A007318 in OEIS).

One interesting property of Pascal’s triangle is the generation of binomials.
To calculate , you can look at the 𝟦-th row (listed above and when starting to count at 𝟢) and determine

This program generates Pascal’s sequence in a rather unusual shape, looking a bit like a crown.

To get more information about Pascal’s triangle, check out this Wikipedia entry.

^[1]

Palindromic Primes

2016-03-23, post № 110

mathematics, programming, Python, #generating, #numbers, #palindrome, #palindromes, #palindromic numbers, #prime numbers, #prime palindromes, #symmetric numbers, #symmetry

TheOnlinePhotographer has published a post to celebrate 𝟣𝟩𝟣𝟩𝟣𝟩 comments and was amused by the number’s symmetry.
A great comment by Lynn pointed out that this number is indeed an interesting number but not symmetrical.
Symmetrical numbers or words — also called palindromes — are defined as being the same read forwards or backwards. Examples for palindromic words are “radar”, “noon” or “level”. Palindromic numbers are 𝟥, 𝟦𝟢𝟦 or 𝟣𝟩𝟤𝟤𝟩𝟣.

Lynn then went further and checked if 𝟣𝟩𝟣𝟩𝟣𝟩 is at least a prime^[1]. The number sadly has five distinct prime factors ().

So Lynn wondered what the next palindromic prime would be.
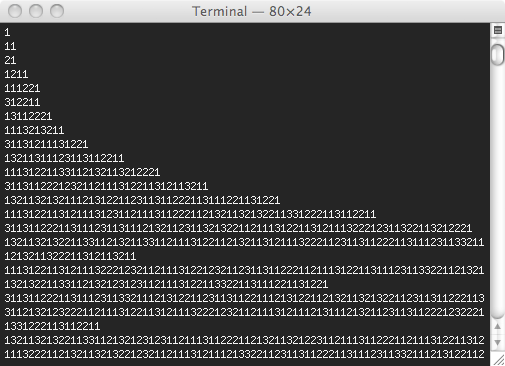
To answer this question, I wrote this little Python program to check for palindromic primes. The first 𝟣𝟤𝟢 palindromic primes are shown below.
Based on this list, the smallest palindromic prime larger than 𝟣𝟩𝟣𝟩𝟣𝟩 is 𝟣𝟢𝟢𝟥𝟢𝟢𝟣.

      3,       5,       7,      11,     101,     131,     151,     181,
    191,     313,     353,     373,     383,     727,     757,     787,
    797,     919,     929,   10301,   10501,   10601,   11311,   11411,
  12421,   12721,   12821,   13331,   13831,   13931,   14341,   14741,
  15451,   15551,   16061,   16361,   16561,   16661,   17471,   17971,
  18181,   18481,   19391,   19891,   19991,   30103,   30203,   30403,
  30703,   30803,   31013,   31513,   32323,   32423,   33533,   34543,
  34843,   35053,   35153,   35353,   35753,   36263,   36563,   37273,
  37573,   38083,   38183,   38783,   39293,   70207,   70507,   70607,
  71317,   71917,   72227,   72727,   73037,   73237,   73637,   74047,
  74747,   75557,   76367,   76667,   77377,   77477,   77977,   78487,
  78787,   78887,   79397,   79697,   79997,   90709,   91019,   93139,
  93239,   93739,   94049,   94349,   94649,   94849,   94949,   95959,
  96269,   96469,   96769,   97379,   97579,   97879,   98389,   98689,
1003001, 1008001, 1022201, 1028201, 1035301, 1043401, 1055501, 1062601, ...

Thus it takes more comments to reach the closest palindromic prime.

The sequence of palindromic primes is number A002385 in the On-line Encyclopedia of Integer Sequences (OEIS).

RGB Color Cube

2016-03-19, post № 109

programming, Pygame, Python, #16777216, #256**3, #all rgb, #blue, #colors, #every rgb color, #green, #red

Listing the red part on the 𝑥-axis, the green part on the 𝑦-axis and the blue part on the 𝑧-axis, this program displays all the 𝟣𝟨𝟩𝟩𝟩𝟤𝟣𝟨^[1] colors rgb can display.
The 𝑧-axis is shown over time, visually going through a cube of colors.

Surfing

2016-03-12, post № 108

art, #animated, #animated gif, #beach, #board, #flip, #gif, #ocean, #surf, #surf board, #wave

The little pixel guy tries himself at surfing.

Look-and-Say Sequence

2016-03-05, post № 107

mathematics, programming, Python, #approx., #approximating, #approximation, #John Conway, #lambda, #number sequence, #sequence

An interesting nonmathematical sequence which yet has interesting mathematical properties is the Look-and-say sequence.
As every good sequence it starts with a 𝟣. From there you get each next entry by looking at the previous and saying it. The next entry will thus be “one 𝟣” or 𝟣𝟣. From there “two 𝟣” or 𝟤𝟣, then “one 𝟤; one 𝟣” or 𝟣𝟤𝟣𝟣, “one 𝟣; one 𝟤; two 𝟣” or 𝟣𝟣𝟣𝟤𝟤𝟣 and so on.

Generating the Sequence

The mathematical property, although, does not lie in the entry’s value, but rather in its length.

Calculating the Length of each Entry

The interesting thing about the length is, that it approximately grows by 𝜆 each time.
This constant 𝜆 can be calculated by getting the real root of a degree 𝟩𝟣 polynomial (see Nathaniel Johnston’s post for further information) or be approximated by dividing entries.

Approximating 𝜆