Look-and-Say Sequence

2016-03-05, post № 107

mathematics, programming, Python, #approx., #approximating, #approximation, #John Conway, #lambda, #number sequence, #sequence

An interesting nonmathematical sequence which yet has interesting mathematical properties is the Look-and-say sequence.
As every good sequence it starts with a 𝟣. From there you get each next entry by looking at the previous and saying it. The next entry will thus be “one 𝟣” or 𝟣𝟣. From there “two 𝟣” or 𝟤𝟣, then “one 𝟤; one 𝟣” or 𝟣𝟤𝟣𝟣, “one 𝟣; one 𝟤; two 𝟣” or 𝟣𝟣𝟣𝟤𝟤𝟣 and so on.

Generating the Sequence

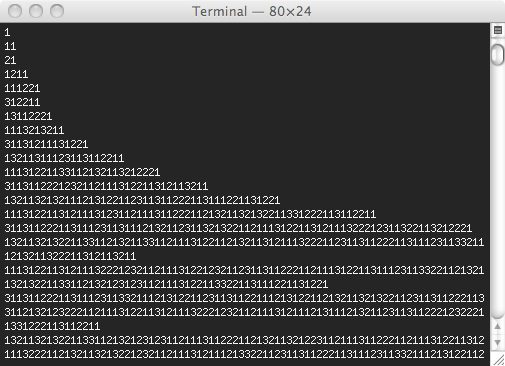
The mathematical property, although, does not lie in the entry’s value, but rather in its length.

Calculating the Length of each Entry

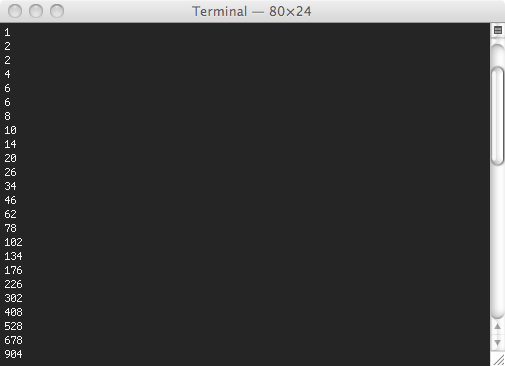
The interesting thing about the length is, that it approximately grows by 𝜆 each time. $\big(\lambda=1.303577269034\dots\big)$
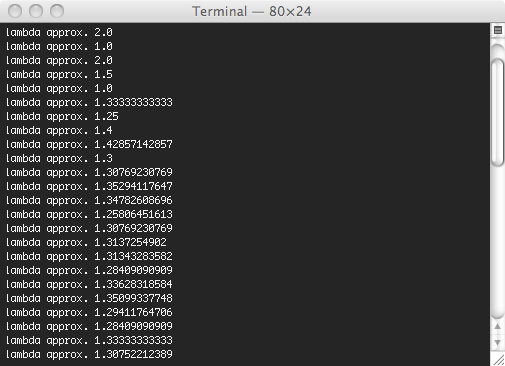
This constant 𝜆 can be calculated by getting the real root of a degree 𝟩𝟣 polynomial (see Nathaniel Johnston’s post for further information) or be approximated by dividing entries. $\big(\lambda=\frac{\text{entry}_{n+1}}{\text{entry}_{n}}\text{ for }n\rightarrow\infty\big)$

Approximating 𝜆

Source code: look-and-say-sequence.py

Extra assets: look-and-say-sequence-v2.py, look-and-say-sequence-v3.py, look-and-say-sequence_extra.py, look-and-say-sequence_beginning.pdf, look-and-say-sequence_beginning.tex