JClock VIII

2016-07-30, post № 135

programming, Pygame, Python, #clock, #complex number, #hour, #minute, #plane, #time

Interpreting the hour hand on a clock as a two-dimensional object on a plane, the hand’s tip can be seen as a complex number.
This clock converts the hour hand’s position into a complex number, sets the number’s length to the current minutes and displays it in the form $a+b\cdot i$ .
The angle 𝜑 is determined by the hours passed ( $\frac{2\cdot\pi\cdot\text{hour}}{12}=\frac{\pi\cdot\text{hour}}{6}$ ) but has to be slightly modified because a complex number starts at the horizontal axis and turns anti-clockwise whilst an hour hand starts at the vertical axis and turns — as the name implies — clockwise. Thus, $\varphi=(2\cdot\pi-\frac{\pi\cdot\text{hour}}{6})+\frac{\pi}{2}=(\frac{15-\text{hour}}{6})\cdot\pi$ .

The complex number’s length is simply determined by the minutes passed. Because the length must not be equal to 𝟢, I simply add 𝟣: $|z|=k=\text{minute}+1$ .
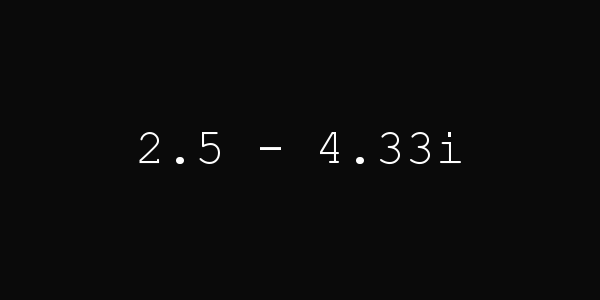
Lastly, to convert a complex number of the form $k\cdot e^{\varphi\cdot i}$ into the form $a+b\cdot i$ , I use the formula $k\cdot(\cos{\varphi}+\sin{\varphi}\cdot i)=a+b\cdot i$ .

Source code: jclock-viii.py